Dragon

业精于勤荒于嬉

0%

你真的会二分查找吗？

发表于 更新于 分类于

二分查找

  • 二分查找是一个基础的算法，也是面试中常考的一个知识点。二分查找就是将查找的键和子数组的中间键作比较，如果被查找的键小于中间键，就在左子数组继续查找；如果大于中间键，就在右子数组中查找，否则中间键就是要找的元素。

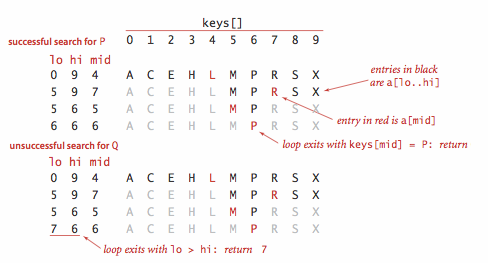
    （图片来自《算法-第4版》）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 二分查找，找到该值在数组中的下标，否则为-1
static int binarySearch(int[] array, int key) {
    int left = 0;
    int right = array.length - 1;
    
    // 这里必须是 <=
    while (left <= right) {
        int mid = (left + right) / 2;
        if (array[mid] == key) {
            return mid;
        } else if (array[mid] < key) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

每次移动left和right指针的时候，需要在mid的基础上+1或者-1，防止出现死循环，程序也就能够正常运行

注意：代码中的判断条件必须是 while (left <= right)，否则的话判断条件不完整，
比如：array[3] = {1, 3, 5}; 待查找的键为5，此时在(low < high)条件下就会找不到，因为low和high相等时，指向元素5，但是此时条件不成立，没有进入while()中。

二分查找的变种

  • 关于二分查找，如果条件稍微变换一下，比如：数组之中的数据可能可以重复，要求返回匹配的数据的最小（或最大）的下标；更进一步，需要找出数组中第一个大于key的元素（也就是最小的大于key的元素）的下标，等等。这些，虽然只有一点点的变化，实现的时候确实要更加的细心。
  • 二分查找的变种和二分查找原理一样，主要就是变换判断条件（也就是边界条件），如果想直接看如何记忆这些变种的窍门，请直接翻到本文最后。下面来看集中二分查找变种的代码：

查找第一个与key相等的元素

  • 查找第一个相等的元素，也就是说等于查找key值得元素有好多个，返回这些元素最左边的元素下标。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    // 查找第一个相等的元素
    static int findFirstEqual(int[] array, int key) {
        int left = 0;
        int right = array.length - 1;
        
        // 这里必须是 <=
        while (left <= right) {
            int mid = (left + right) / 2;
            if (array[mid] >= key) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        if (left < array.length && array[left] == key) {
            return left;
        }
        return -1;
    }

    查找最后一个与key相等的元素

  • 查找最后一个相等的元素，也就是说等于查找key值得元素有好多个，返回这些元素最右边的元素的下标。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    // 查找最后一个相等的元素
    static int findLastEqual(int[] array, int key) {
        int left = 0;
        int right = array.length - 1;
        
        // 这里必须是 <=
        while (left <= right) {
            int mid = (left + right) / 2;
            if (array[mid] <= key) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        if (right >= 0 && array[right] == key) {
            return right;
        }
        return -1;
    }

    查找最后一个等于或者小于key的元素

  • 查找最后一个等于或者小于key的元素，也就是说等于查找key值的元素有好多个，返回这些元素最右边的元素下标；如果没有等于key值得元素，则返回小于key的最右边元素下标。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    // 查找最后一个等于或者小于key的元素
    static int findLastEqualSmaller(int[] array, int key) {
        int left = 0;
        int right = array.length - 1;
        
        // 这里必须是 <=
        while (left <= right) {
            int mid = (left + right) / 2;
            if (array[mid] > key) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return right;
    }

    查找最后一个小于key的元素

  • 查找最后一个小于key的元素，也就是说返回小于key的最右边元素的下标。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    // 查找最后一个小于key的元素
    static int findLastSmaller(int[] array, int key) {
        int left = 0;
        int right = array.length - 1;
        
        // 这里必须是 <=
        while (left <= right) {
            int mid = (left + right) / 2;
            if (array[mid] >= key) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return right;
    }

    查找第一个等于或者大于key的元素

  • 查找第一个等于或者大于key的元素，也就是说等于查找key值得元素有好多个，返回这些元素最左边的元素下标；如果没有等于key值的元素，则返回大于key的最左边元素下标。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    // 查找第一个等于或者大于key的元素
    static int findFirstEqualLarger(int[] array, int key) {
        int left = 0;
        int right = array.length - 1;
        
        // 这里必须是 <=
        while (left <= right) {
            int mid = (left + right) / 2;
            if (array[mid] >= key) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

    查找第一个大于key的元素

  • 查找第一个大于key的元素，也就是说返回大于key的最左边元素下标。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    // 查找第一个大于key的元素
    static int findFirstLarger(int[] array, int key) {
        int left = 0;
        int right = array.length - 1;
        
        // 这里必须是 <=
        while (left <= right) {
            int mid = (left + right) / 2;
            if (array[mid] > key) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

    二分查找变种总结

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    // 这里必须是 <=
    while (left <= right) {
        int mid = (left + right) / 2;
        if (array[mid] ? key) {
            // ...right = mid - 1;
        } else {
            // ...left = mid + 1;
        }
    }
    return xxx;
  • 二分查找变种较多，不过他们的“套路”是一样的，以上代码就是其套路，如何快速写出二分查找的代码，只需按照以下步骤即可：

  1. 首先判断出是返回left，还是返回right

    • 因为我们知道最后跳出while (left <= right)循环条件是right < left，且right = left - 1。最后right和left一定是卡在“边界值”的左右两边，如果是比较值为key，查找小于等于（或者是小于）key的元素，则边界值就是等于key的所有元素的最左边那个，其实应该返回left。
    • 以数组{1, 2, 3, 4, 5}为例，如果需要查找第一个等于或者小于3的元素下标，我们比较的key值是3，则最后left和right需要满足以下条件：
    • 我们比较的key值是3，所以此时我们需要返回left。

  2. 判断出比较符号

    1
    2
    3
    4
    5
    6
    int mid = (left + right) / 2;
    if (array[mid] ? key) {
        // ...right = xxx;
    } else {
        // ...left = xxx;
    }
  • 也就是这里的if (array[mid] ? key)中的判断符号，结合步骤1和给出的条件，如果是查找小于等于key的元素，则知道应该使用判断符号>=，因为是要返回left，所以如果array[mid]等于或者大于key，就应该使用>=，以下是完整代码
    1
    2
    3
    4
    5
    6
    7
    // 查找小于等于key的元素
    int mid = (left + right) / 2;
    if (array[mid] >= key) {
        right = mid - 1;
    } else {
        left = mid + 1;
    }

参考：